66 Comments
Please note: the table used on this page does not reflect the finalized Grant Support Index values, discussed in the May 2 2017 blog, “Implementing Limits on Grant Support to Strengthen the Biomedical Research Workforce“. Community input will be used in developing the final Grant Support Index. – Open Mike blog team, May 8, 2017.
———————————————————————————————————————–
On this blog we previously discussed ways to measure the value returned from research funding. The “PQRST” approach (for Productivity, Quality, Reproducibility, Sharing, and Translation) starts with productivity, which the authors define as using measures such as the proportion of published scientific work resulting from a research project, and highly cited works within a research field.
But these factors cannot be considered in isolation. Productivity, most broadly defined, is the measure of output considered in relation to several measures of inputs. What other inputs might we consider? Some reports have focused on money (total NIH funding received), others on personnel. And all found evidence of diminishing returns with increasing input: among NIGMS grantees receiving grant dollars, among Canadian researchers receiving additional grant dollars, and among UK biologists overseeing more personnel working in their laboratories.
It might be tempting to focus on money, but as some thought leaders have noted, differing areas of research inherently incur differing levels of cost. Clinical trials, epidemiological cohort studies, and research involving large animal models are, by their very nature, expensive. If we were to focus solely on money, we might inadvertently underestimate the value of certain highly worthwhile investments.
We could instead focus on number of grants – does an investigator hold one grant, or two grants, or more? One recent report noted that more established NIH-supported investigators tend to hold a greater number of grants. But this measure is problematic, because not all grants are the same. There are differences between R01s, R03s, R21s, and P01s that go beyond the average amount of dollars each type of award usually receives.
Several of my colleagues and I, led by NIGMS director Jon Lorsch – chair of an NIH Working Group on Policies for Efficient and Stable Funding – conceived of a “Research Commitment Index,” or “RCI.” We focus on the grant activity code (R01, R21, P01, etc) and ask ourselves about the kind of personal commitment it entails for the investigator(s). We start with the most common type of award, the R01, and assign it an RCI value of 7 points. And then, in consultation with our NIH colleagues, we assigned RCI values to other activity codes: fewer points for R03 and R21 grants, more points P01 grants.
Table 1 shows the RCI point values for a PI per activity code and whether the grant has one or multiple PIs.
Table 1:
| Activity Code | Single PI point assignment | Multiple PI point assignment |
| P50, P41, U54, UM1, UM2 | 11 | 10 |
| Subprojects under multi-component awards | 6 | 6 |
| R01, R33, R35, R37, R56, RC4, RF1, RL1, P01, P42, RM1, UC4, UF1, UH3, U01, U19, DP1, DP2, DP3, DP4 | 7 | 6 |
| R00, R21, R34, R55, RC1, RC2, RL2, RL9, UG3, UH2, U34, DP5 | 5 | 4 |
| R03, R24, P30, UC7 | 4 | 3 |
| R25, T32, T35, T15 | 2 | 1 |
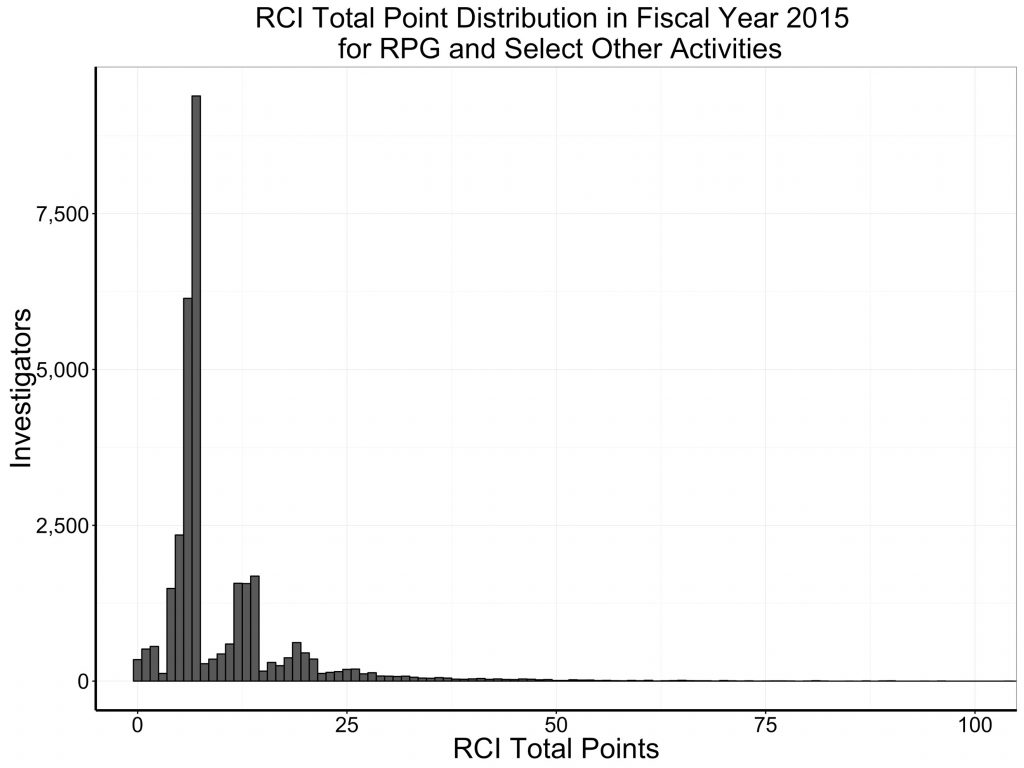
Figure 1 shows by a histogram the FY 2015 distribution of RCI among NIH-supported principal investigators. The most common value is 7 (corresponding to one R01), followed by 6 (corresponding to one multi-PI R01). There are smaller peaks around 14 (corresponding to two R01s) and 21 (corresponding to three R01s).
Figure 1:
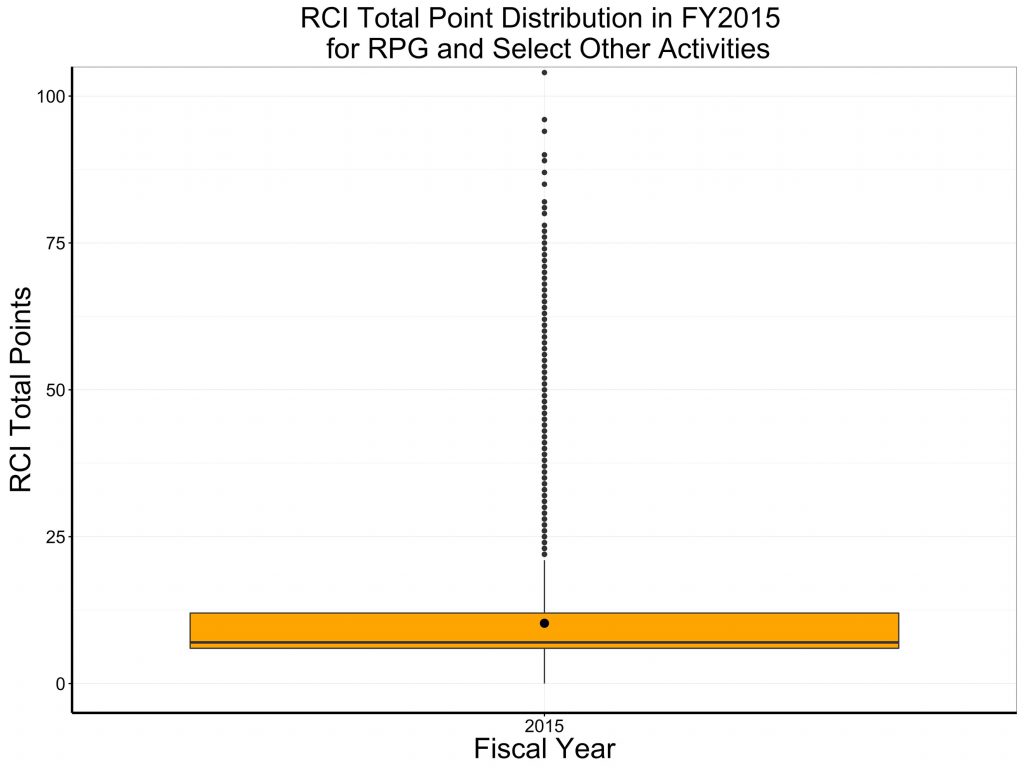
Figure 2 uses a box-plot format to show the same data, with the mean indicated by the larger dot, and the median indicated by the horizontal line. The mean of 10.26 is higher than the median of 7, reflecting a skewed distribution.
Figure 2:
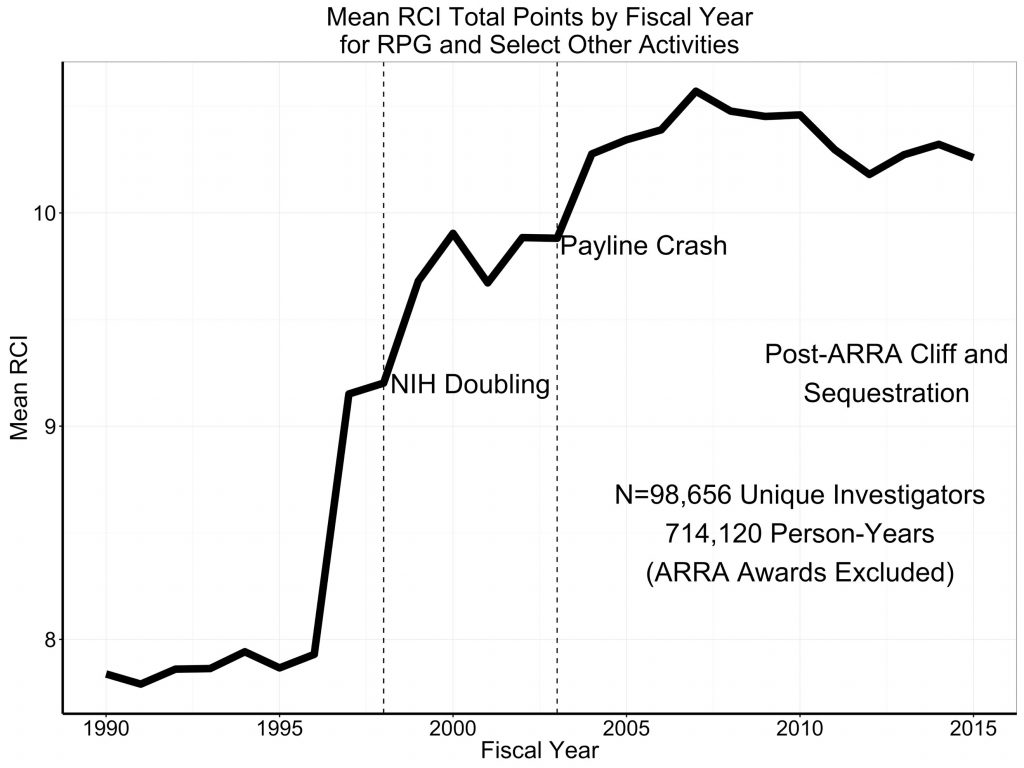
From 1990 through 2015 the median value of RCI remained unchanged at 7 – the equivalent of one R01. But, as shown in Figure 3, the mean value changed – increasing dramatically as the NIH budget began to increase just before the time of the NIH doubling.
Figure 3:
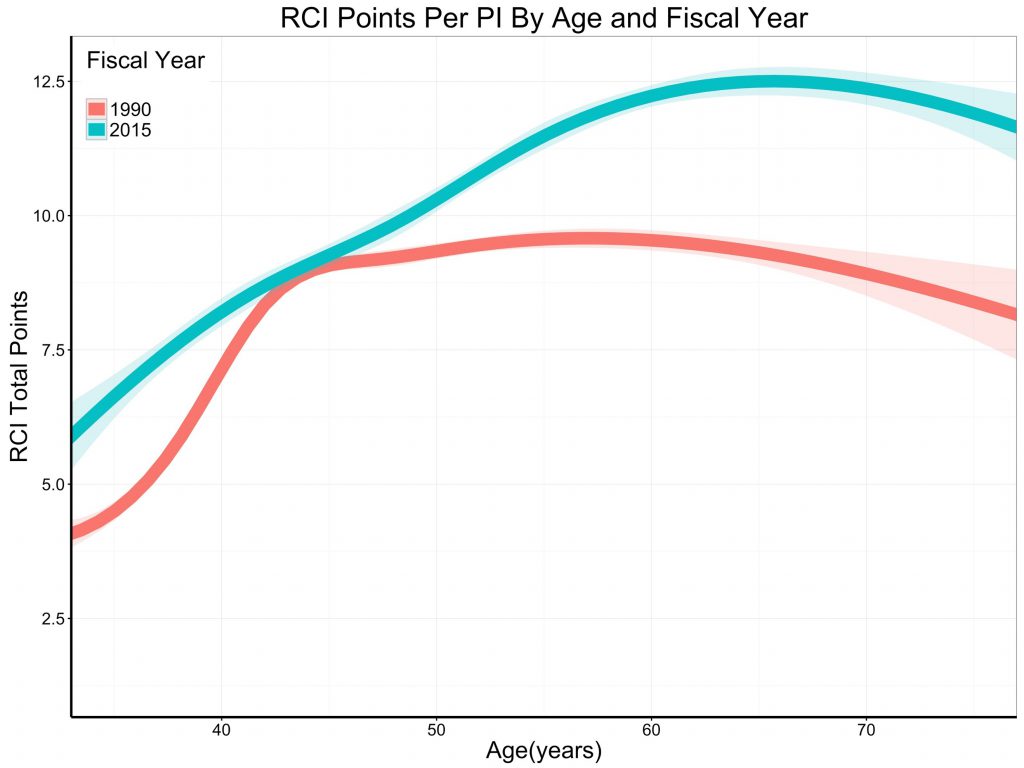
Figure 4 shows the association of RCI and the age of PIs; the curves are spline smoothers. In 1990, a PI would typically have an RCI of slightly over 8 (equivalent to slightly more than one R01) irrespective of age. In 2015, grant support, as measured by RCI, increased with age.
Figure 4:
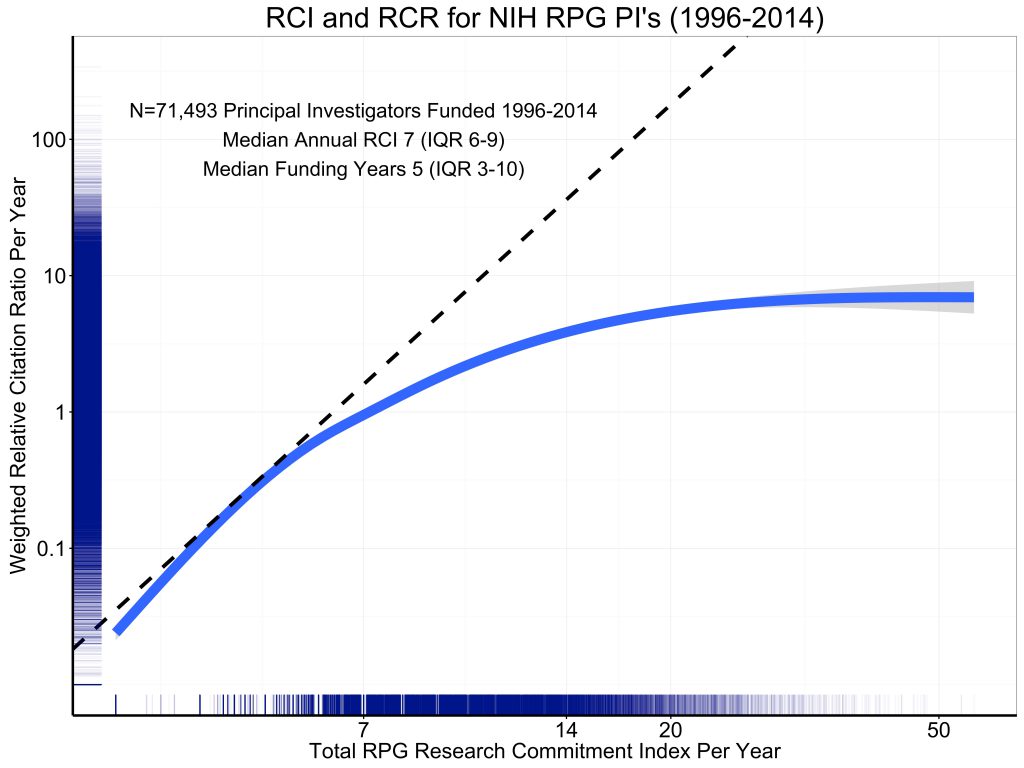
We now turn to the association of input, as measured by the RCI, with output, as measured by the weighted Relative Citation Ratio (RCR). We focus on 71,493 unique principal investigators who received NIH research project grant (RPG) funding between 1996 and 2014. We focus on RPGs since these are the types of grants that would be expected to yield publications and because the principal investigators of other types of grants (e.g. centers) won’t necessarily be an author on all of the papers that come out of a center. For each NIH RPG PI, we calculate their total RCI point values for each year, and divide it by the total number of years of support. Thus, if a PI held one R01 for 5 years, their RPG RCI per year would be 7 ((7 points * 5) / (5 years). If a PI held two R01s for 5 years (say 2000-2004) and during the next two years (say 2005 and 2006) held one R21, their RPG RCI per year would be 11.43 [(14 points * 5) + (5 points * 2)] / (7 years).
Figure 5 shows the association of grant support, as measured by RPG RCI per year, with productivity, as assessed by the weighted Relative Citation Ratio per year. The curve is a spline smoother. Consistent with prior reports, we see strong evidence of diminishing returns.
Figure 5:
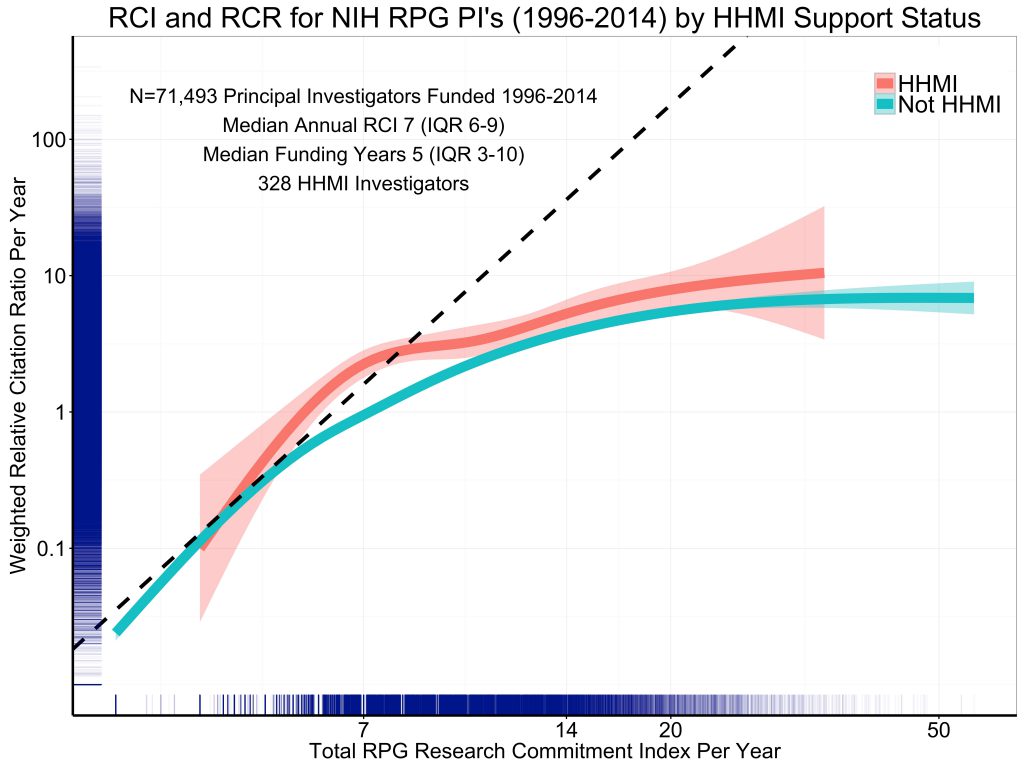
A limitation of our analysis is that we focus solely on NIH funding. As a sensitivity test, we analyzed data from the Howard Hughes Medical Institute (HHMI) website and identified 328 unique investigators who received NIH RPG funding and HHMI funding between 1996 and 2014. Given that these 328 investigators received both NIH grants and HHMI support (which is a significant amount of long term person-based funding), they would be expected to be highly productive given the additive selectivity of receiving support from both NIH and HHMI. As would be expected, HHMI investigators had more NIH funding (measured as total RCI points, annual RCI, number of years with NIH funding) and were more productive (more NIH-funded publications, higher weighted RCR, higher annual RCR, and higher mean RCR).
Figure 6 shows annual weighted RCR by annual RCI, stratified by whether the PI also received HHMI funding. As expected, HHMI investigators have higher annual weighted RCR for any given RCI, but we see the same pattern of diminishing returns.
Figure 6:
Putting these observations together we can say:
- We have constructed a measure of grant support, which we call the “Research Commitment Index,” that goes beyond simple measures of funding and numbers of grants. Focusing on funding amount alone is problematic because it may lead us to underestimate the productivity of certain types of worthwhile research that are inherently more expensive; focusing on grant numbers alone is problematic because different grant activities entail different levels of intellectual commitment.
- The RCI is distributed in a skewed manner, but it wasn’t always so. The degree of skewness (as reflected in the difference between mean and median values) increased substantially in the 1990s, coincident with the NIH budget doubling.
- Grant support, as assessed by the RCI, increases with age, and this association is stronger now than it was 25 years ago.
- If we use the RCI as a measure of grant support and intellectual commitment, we again see strong evidence of diminishing returns: as grant support (or commitment) increases, productivity increases, but to a lesser degree.
- These findings, along with those of others, suggest that it might be possible for NIH to fund more investigators with a fixed sum of money and without hurting overall productivity.
At this point, we see the Research Commitment Index as a work in progress and, like the Relative Citation Ratio, as a potentially useful research tool to help us better understand, in a data-driven way, how well the NIH funding process works. We look forward to hearing your thoughts as we seek to assure that the NIH will excel as a science funding agency that manages by results.
I am grateful to my colleagues in the OER Statistical Analysis and Reporting Branch, Cindy Danielson and Brian Haugen in NIH OER, and my colleagues on the NIH Working Group on Policies to Promote Efficiency and Stability of Funding, for their help with these analyses.



So what are the next steps? What does the NIH intend to do with this information?
Is it fair to log scale the y-axis on figures 5 and 6? It looks like a linear scale would paint a far different picture.
I applaud these kinds of analyses, which are not easy to do. Good decision making can only arise from good facts. Thanks for trying to get the facts straight.
The data seem to contradict the author’s conclusions. The data are distorted by using log or semi log plots and differential scaling of the X and Y axes in figures 5 and 6. Contrary to the claim of “diminishing returns”, it appears that an investigator with RCI of 7 has a weighted citation ratio of 1. With a doubling of RCI to 14 the citation ratio increases by about 3-fold to 3 (hard to tell exact amount). So there are actually increasing returns, not decreasing. Am I missing something here? If this is true, then an investigator who is awarded a second grant uses that money more productively than if the money were awarded to a different investigator awarded with a single grant.
You make an excellent point about the difference between 1 and 2 R01’s, where productivity appears to jump considerably. However, the curve genuinely flattens after 2 R01’s, which may be the more important issue. The small number of people with more than 2 R01’s aren’t continuing the upward trajectory of publications, which supports the idea of capping funding around 3 R01s.
This is an interesting approach. However I worry that exploratory work that generates new hypotheses may take longer (and therefore be seen as riskier) than work that continues defining important mechanisms in previously explored processes. Hence, the approach you outline may end up reinforcing the culture of risk aversion in NIH supported research.
This is potentially very significant. It does indicate that rewarding a a few investigators with large amounts of funding is not necessarily the best idea. More investigators can be funded while maintaining or improving overall productivity per grant. While a hard cap, like “no more than x grants per PI” is probably not wise, some sort of penalty for an equivalent of 2 R01s (14 RPG points) per PI may be useful.
Agree 100%. A bonus could be added directly to the percentile score of currently unfunded investigators if they have appropriate institutional support and access to facilities. A smaller bonus could even be added for those with one R01, but no bonus for those with two R01’s or the equivalent.
The Log scale on the Y-axis could be potentially misleading for Fig 5 and 6. It should have been simple enough to have presented the linear scale, which should give a better readout between productivity vs RCI. Please consider adding them here.
Log scale use is a clear way to benefit one side of argument. Benefit of more grants minimized as presented and likely benefit possible in 2R01 range is being hidden. Perhaps more importantly output is limited to just publications, treating all as equal both in impact and even data quality and quantity. If so just publish short papers with 2-3 simple figs rather than more complete stories of greater use and impact. Reviewers are less critical and forgiving also. But your output would go up when in real terms quality goes down. A Science paper can have 2-3 fold more data in it including supplement than average even top line journal (for ex. JBC) and twice that for bottom 50% journals. What about papers that open new fields or are truly paradigm shifting? When grants get bigger like P01 the absolute number of papers may suffer but number of authors per publication may increase as well the synergy and overall progress in the field. Also is # of papers only output or can getting to clinical testing really be even a more noteworthy goal. Need to be careful that we do not simply hunt for readouts that make the feel good case to the masses. Need a balance between unbridled capitalism where the young may suffer and simplistic socialism where ambitious “real deal” achievers are shackled and deterred from a timely and truly meaningful advancement. So much more needs to be considered and hopefully will be done thoroughly before any “hasty executive order” – little humor?
Comparison between 1990 and 2015 in Figures 3 and 4 need to be interpreted with caution. The nature of investigator employment has changed dramatically between these points in time. “Hard money” positions supported by research institutions was far more common in 1990 than they are now, which effectively subsidized the NIH investment in productivity. In 2015, successful researchers, by and large, must obtain a much higher proportion of their salaries from external funding. Thus it is not at all surprising to see greater RCI with increasing age and career advancement. With these changes in how investigators are funded, it is not clear that flattening the RCI by age curve is feasible while maintaining the workforce and productivity.
It is import to consider that institutional funding (e.g. from research universities) is a significant, but relatively fixed, per-PI cost of the total research enterprise. If NIH funds more PI’s this cost will increase significantly. For example, if NIH funds twice as many PIs with the same amount of money, this cost to the institutions employing PIs will roughly double. It is not clear that the employing institutions will be willing or able to shoulder this cost.
Have to agree with others, simply post Fig 5 with linear scale on both axis. Without that, it is hard to tell exactly what’s happening. One can guesstimate that it is roughly linear, hence one investigator with 3 R01s produces about the same as 3 investigators with 1 R01 each. If that is the case, the conclusion that “it might be possible for NIH to fund more investigators with a fixed sum of money and without hurting overall productivity.” is supported.
Thank you for this analysis and for introducing these interesting metrics. Would it be possible to do the analysis for clinical versus basic research? I think lumping both together may not give an accurate picture.
Just want to echo the above comments that using log scale on the y-axis in Figures 5 and 6 is disingenuous. A logarithmic shape of both curves with only the y-axis on log scale suggests a roughly linear relationship with a linear scale on both axes.
Please also add consideration of P60 awards, which I would recommend are equivalent to P50.
You should make these easier for use to download/print so we can distribute and discuss with our colleagues.
If these data are plotted on a linear scale, the relation appears to be quite linear. The ‘diminishing’ effect seems to vanish – at least in the range of 6-20 for RCI. The dashed line seems to suggest that the weighted citation ratio should be 1 for RCI of 6 but >100 for RCI of 20 to not have diminishing return on investment? Please clarify!
Were any RCI points assigned to Activity Codes that are not listed in Table 1? I am looking into replicating something like this for my institution, and am interested in whether you ignored Activity Codes outside of those listed or if you simply assigned all others an average RCI value.
Plausible … “PQRST” approach will push big data fabrication labs to assess the translational applications of the statistical outcomes….!
This system penalizes collaborative science done in P50, P0-1 and other multi-PI grants. The NIH should build incentives into the scoring to promote collaborative and interdisciplinary science, not penalize it. Collaborative and interdisciplinary science is often more productive, more innovative, and as such represents a more effective way to do science. Thus, it should be promoted, not discouraged. The individual budget for scientists participating in P0-1 and P50 is much smaller than for a R0-1. Thus, participating in collaborative science according to the new scoring would damage the investigators chances to fund his/her own science. Exactly the wrong thing to do.
Also, training grant directors should get at least a plus of 2 points given how much work it is. Again, vital work, contributions to the institution, mentoring the next generation of scientists are penalized, not encouraged.
This is a free country build on the strengths and freedom of the individual. By limiting grants one person can receive, you also limit our very best. No matter what the average curve looks like. Yes, we should evaluate the productivity of an investigator and decide how many grants he/her deserve, but have one rule fits all is really the sort of socialism that fails the individual.
I agree in principle with the goals here, but would like to see a more nuanced analysis, based not just on number of awards, but total direct costs to the PI. For example, a typical R01 budget is not 7/5 times that of an R21. In addition some Institutes apply broad cuts to budgets of approved awards, while others do not.
Unless I missed something, it appears that this points model highly disincentivizes the benefits from the interdisciplinary multi-PI approach. For example, a single PI R01 investigator will be assessed 7 points for an R01, but two investigators that are multi-PI and might split a budget 50%/50% each get 6 points. What about a MPI R01 grant with 3 MPIs, are they still all assessed 6 points each? This seems to highly disincentivize the multi-PI approach since instead of being assessed half the points for what presumably is half the budget, a multi-PI is assessed almost the same (6 vs 7) points. It will be less attractive to work with your collaborators on a multi-PI project which will “cost” 6 points but will only provide a fraction of the grant budget to support your lab’s effort. Maybe this is only a concern for scientist intending to be part of more than one grant/collaboration, but wouldn’t splitting the number of total points across the number of MPIs on a project make more sense?
I have a similar concern about the way the allocation of points for MPI grants under this plan seems to strongly discourage team science. This is unfortunate given the frequent benefits of taking a multidisciplinary and collaborative approach. In addition to the points made by Paul, I also found it interesting to think about this from the NIH Commitment perspective: if the purpose of the Research Commitment Index is to show us the NIH’s resources are distributed amongst grant awardees it seem strange that the financial commitment represented by a single award multiplies rather quickly if there are multiple PI’s even though the total resources committed remain the same.
Completely agree. There is no data shown to justify the proposed penalty on multi-PI approach. In fact, complex biomedical research requires multidisciplinary team work. Particularly, translational research needs both basic scientists and clinicians. A fair point system for m-PI should be 7/m.
I share the concern that the proposed point system would act as a powerful disincentive to collaboration.
While I agree in concept, the point system here have several flaws. First, the points given for the smaller grants are way too high. For instance R21s are approximately have the funding of a modular R01 (and most are not modular anymore), and yet is 5/7th of the points. R03s are even less money, and are still at 4 points. These high levels of points will limit innovative and high risk high reward science, but making the point burden too high.
Second, it is totally ridiculous to give any points for T32 PIs! T32 PIs don’t even get salary support from the T32, and the institution is required to support the effort. As a T32 PI, I can attest to the amount of time it takes to run a T32 program, and that it is actually a negative for my research endeavor. Even charging 1 point, limits my ability to fund my laboratory by 1 full R01 in this proposed system! In fact, as stated by Dr. Mothes above, NIH should actually give T32 PIs and similar training grants, points back for our citizenship to developing the early stage investigators that this policy is trying to help!
Finally, I agree with Dr. Mothes that projects with restricted budgets such as PPGs and U grants need to have lower points as these are smaller projects and not equal to R01s.
I agree with Anne Sperling, that the new “Rule of 21” has many flaws, and implementation should be delayed to allow for community discussion and feedback, and revision.
I fully agree with many of the points made here, particularly the protest of disincentives for collaborative work and especially for supporting training grants!! While I can appreciate the logic about spreading the wealth, I fail to see the logic for penalizing those who participate in T32s! This is essentially community service, supporting the next generation of scientists, and brings no direct funds to the lab of the PIs. The messaging for Multi-PI grants also seems warped: collaborative work should be encouraged as it often brings about transformative breakthroughs and is heavily penalized under the proposed GSI system. Some statement towards these two implicit consequences (reduced support of training grants and fewer collaborative grants) should be made, as they seem incompatible with the stated mission of this policy.
I would be very concerned about all of this analysis. If the NIH wants to use any of these metrics, they need to make the methodology and data fully transparent, ideally in a published paper. This is exactly the standard we as scientists are required to meet,
We cannot possibly tell how the analysis and data shown in this post were generated and how the data were pre-selected. We need a clear understanding of confounders in such analyses, and it absolutely must be subjected to peer review. In my opinion, all NIH policy documents that purport to being quantitative need to be peer reviewed. Otherwise, lets just call in an pre-judged opinion.
The proposed research commitment index will decimate translational and transdisciplinary research. The last years have seen accelerated translation of basic research into clinical practice and this trend is expected to become ever more important for the NIH mission, e.g. in precision medicine and liquid biospies. It relies on the participation of productive basic scientists in clinical cooperative groups, multi-investigator programmatic grants and the NIH NCATS initiative. Being limited on the number of grants to hold, the most successful NIH investigators will no longer be able to afford participating in these initiatives.
The current point award system is flawed. In addition to comments on R21/RO3/T32 noted above, the award of 6 points on multi-PI grants is not based on the consideration of the efforts and budget of the multi-PIs on a particular RO1. In the current model, a limited effort with smaller budget for a multi-PI is still awarded a 6 point. This does not make any sense and would absolutely kill the collaborative and interdisciplinary science. Why would one submit a multi-PI grant with limited budget to strike out 6 points when one can submit a single PI RO1 at the cost of just 1 more point?
Additionally, since the current NIH think tank wants to implement GSI point system rather than dollar amounts, there will be substantial increase in larger RO1 submissions rather than modular ones with defined 250K/year budget. Will this necessarily free up NIH money?
This is a very problematic plan in many ways, but I will focus on P50’s and U54’s. The amount of funding allowed on these has gone down, so less money is left for projects. If such high scores are given to the PIs, they would have to take a very substantial portion of their effort to be a PI, leaving little for actual research, when the real work is done by the individual investigators. The PI’s here organize others to do interactive and multidisciplinary work. This scoring system would effectively preclude a program leader from having their own research program, and these applications would disappear, and with them, multidisciplinary and translational research. The effort required for these- 20%, is a reasonable estimate of how much work is required, and is about equivalent to an R01. They should be scored similarly.
Completely agree.
This system is going to totally destroy collaborative research. For example, I am a PI on an multi-PI R01 and only receive $80K in direct costs, yet my effort is important for the work. If this is going to be scored as a 6, then what motivation would I have to participate in such a project? This system is going to force people to write very large budget single PI R01s, and justify the budgets with equipment, supplies and personnel. This will incentivize people to not include collaborators that are increasingly playing a very big role. It also doesn’t take into account large grants that will expire a year down the line. If a grant is disallowed because the points are too high, a lab may be left without money a year into the future for example.
While I applaud the goal of trying to spread out NIH funding more equitably, as noted by many others already, the proposed point system will highly penalize collaborative research; e.g., it would discourage participation in multi-PI P50 grants, which often fund individual PIs at levels lower than R01 funding. If this point system is instituted, most PIs would also stop participating in multi-PI R01s in which he/she plays an essential role, but receives minimal funding. Teaming up with a senior PI on a multi-PI R01 was a way that new investigators could get into the system, but with everyone trying to minimize points, most PIs will be forced to apply for single PI R01s. I predict this system will very negatively affect multi-disciplinary collaborative research and new PIs – surely this is not the intention of the NIH.
I think that like all scientific publications, this data and it’s interpretation should be subjected to peer review by qualified members of the extramural biomedical community of researchers.
There are numerous unanswered questions from the presentation shown above. For example, in the crucial Figure 5, which many have pointed out is plotted on a logarithmic scale that may be misleading, the “weighted relative citation ratio” on the y axis is not defined. However, assuming this means citations for funded programs, the entire logarithmic portion from which they are extrapolating peaks extends to about 0.5, which seems to imply this part of the plot is based on grants that resulted in no publications of any merit. If this is the case, and I can’t be sure since there is no appropriate Figure legend, or methods section, nothing below 1 should have been funded – the projects were complete and utter failures. Or maybe these were all instrument grants!
Perhaps the data should have been plotted from 1 upwards on a linear scale. One citation per R01 as the origin! Pretty pathetic by most study section standards, but even accepting that, data seems to make a convincing case that more funding results in more productivity with more impact! The leveling off effect beyond 20 may have some merit, and that could be investigated further. Who can tell without delving into this at a deeper level?
Before the NIH rushes off to cripple all the scientific high fliers and highly collaborative scientists in the country, they should allow their data to be held accountable by the scientific community. This important information should be held to the same standards that we as scientists are held by the NIH and subjected to rigorous peer review. We should insist that they assemble an independent extra mural panel to review this analysis.
From what I have seen so far, I doubt this data will stand up to such scrutiny! If I were referring this blog for publication (and admittedly I have only seen the abstract) I would recommend reject, more suitable for Breitbart news. Maybe others will be more charitable and recommend “major revisions”.
If I were scoring this as an R01 submission, I would recommend a preliminary score of 8 or 9. But maybe there is another reviewer out there who will give this a 3 and we have to discuss it.
Major changes in policy should not be rushed into in such haste. If these analyses are the main basis for this change in policy, then they should be rigorous, transparent and unimpeachable.
I was a little sloppy in the way I wrote my previous comment, but I was angry. Let me reiterate and clarify a few points:
The citation index (RCI) is essentially a citation index (with all the strengths and weaknesses of a citation index as a measure of scientific value) which has been adjusted to reflect average citations between different fields. It has also been normalized to reflect the average productivity of an R01, hence it is set to 1 for an RPG index of 7. However, it is remarkable, and somewhat shocking, how rapidly this falls off below the R01 funding level. Someone with a single R21 is simply not as productive as the average holder of an R01. In the “control” for HHMI investigators, they are showing a huge outperformance for the smaller grants – the opposite of what was stated, and presumably because they have core funding. In any case, to measure the change in productivity with more RPG points, the curves should be plotted on a linear scale since the range is intrinsically limited. After all, even if someone only publishes in Science and Nature and writes copious reviews in Science and Nature, there are only so many citations that can be achieved. Thus, the flattening of curve as the RPG index increases probably reflects an asymptotic approach to the limit of the average citation index for best Journals!
It would be instructive, in fact, to see the actual distributions at various 7 point increments. I’m sure there is a steady skewing to the higher end that is not reflected in the mean values as the RPG scores increase. No doubt there are fancy statistical treatments, well beyond my capacities, that can, and should, be applied to the data. But simple things such as confidence intervals, z-scores etc… will let us know whether these metrics have validity. But assuming the underlying data and metric are ok, the qualitative point is that the data shown does not appear to support the contention that productivity falls with higher RPG scores.
I am also disturbed by the implication in the NIH stance that a cap has to be imposed because the peer review system has failed and is biased towards giving too many resources to the richest laboratories. Yet, the tiny minority of people who manage to get multiple grants suggests that peer review is working perfectly well, that it is extremely difficult win and sustain multiple grants, and that the grants are simply going to the best investigators. As we all know, people go up and down in their careers and the grants held by individuals also fluctuate. That is exactly what you would like to see: a reallocation of resources as productivity and impact, as judged by the peer review system, changes for individuals over time.
If the premise is wrong, than it fair to ask whether the NIH is addressing the right problem using the right tools? Many people have argued that the problems facing junior investigators have arisen because the R01 funding pool has shrunk. What are the trends for the proportion of spending on R01 and the various mechanisms over time? How does productivity change with mechanism? Most importantly, is there a difference in productivity between P01s, R01s awarded via RFAs, and R01s awarded in the open competition? Perhaps the citation metrics the NIH has invented would be better applied to answering these questions. If there are large differences, why not distribute resources from the least successful mechanisms back into the R01 pool? Why not aim to increase the R01 pool by 10 or 20%?
Finally, I strongly agree with the majority of the commentators that using the very flawed RCI point scale to determine a cap will be extremely damaging. The disincentives to collaborate are clear. However, most of the comments were written from the grant holder’s perspective. Let’s also consider the impact of these changes on junior faculty and research associates: The reality is that many talented junior people can’t get grants on their own and they are instead being supported through collaborations with more senior people until they get more established. Certainly at my institution we make a huge effort to bring junior faculty into the grant system in this manner. What will happen to them if their “capped” senior collaborator has to drop several grants? Sadly, many will simply get fired. The points as currently structured will also drive senior people away from altruistic activities like running centers that give developmental support and running training grants. This will further harm the junior investigators.
Finally, let’s work to identify and remove biases in peer review. The current system gives too much authority to the study sections (who do not have a full range of expertise and limited time) and too little chance of rebuttal to the investigator. The system could easily be improved, but that’s another discussion.
Jonathan-no you were not off target at all! Your points are correct-the data wouldn’t pass muster at any good journal, and certainly not at study section. If NIH is going to use this data as a basis for a dramatic change as to how they will fund grants (if this current proposal was enacted as planned, it could be the largest redistribution of R and D dollars in decades), then it should be based on data that is rock solid. I would suggest that the NIH Director and Mike Lauer have these data analyzed by an outside informatics specialist and then that analysis be distributed to the entire NIH community.
As everyone likes to say, lets see the raw data!
As several commenters have noted already, the proposed scale creates strong incentives against activities the research community has always valued. Collaborative research, exploratory work, and outreach and training will all be penalized under the proposed point system.
Assigning points for R25 and T-series awards is particularly damaging. Successful investigators with strong research support should be encouraged to engage in training the next generation. The proposed scheme would instead penalize research programs for providing an important service.
Although I understand the rationale for NIH trying this approach,
once cannot do it simply based on number of grants!!
My 15 year old RO1 grant brings in 150K/year having being cut consecutively each time it is renewed. How is it fair to give the same value of points to one RO1 grant with a budget of 150K/year and another RO1 with a non-modular budget of 400K? It is completely unfair! Please re-think this point system!
This system will penalize everyone who has stayed on track in a field and renewed their RO1 grants over the years instead of switching fields and applying for a new RO1 with a full 250K/year budget.
Also, T32s and other training grants should be given 0 points. Otherwise it will be hard to incentivize good and productive faculty to apply for a T32. These type of faculty are the ones that actually support and mentor trainees successfully.
Another point mentioned above is this system totally dis-incentivizes multiple PI grants. Why not have a mPI grant cost half of the points of a single PI grant? This will incentivize collaboration.
I favor capping PIs at a dollar limit rather than by number of points. This is an absurd system to cap by number of grants. In sum, this will be bad for collaboration and training of graduate students and postdocs.
This is a very short-sighted proposal based on a premise that is not backed by their own data. How would cutting funding from the top 5% of investigators solve the core problem of not having enough money? By redistributing the 10% gained to PIs who are not as successful? Most of the breakthroughs are made by the top investigators and cutting their funding will only hurt the system. Now, if NIH believes that their top 5% best-funded investigators do not do the best science then perhaps improving *review* is in order before invoking well-intentioned but disastrous communist economics.
(1) There is already a system to determine whether an investigator has sufficient bandwidth, it is the percent effort required. NIH program could evaluate if a given investigator is able to perform the work. Some people just have more ideas and work harder, there is no need for an additional cap – we have one in place.
(2) NIH cannot find a correlation between review scores and productivity – this seems like a major issue. Having reviewed a lot, I submit that the correlation may be weak but no correlation suggests that NIH cannot define productivity. Until this serious issue is resolved the entire discussion of funding versus productivity is moot.
(3) If you accept the RCI ratio as a measure of productivity then having two R01s triples productivity compared to a single R01 based on the plot. By the proposal’s logic should funding threshold be lowered after 1 R01?
(4) The point system is too simplistic as many have pointed out: discourages collaboration, centers and training grants. And different R01s bring in different amounts of money so it also discourages investigators who are able support multiple different research programs with modular R01s by counting them as equivalent to large R01s that can bring in twice the money or more.
(5) Data that went into the graphs are old and with biomedical inflation and the number of experiments required for a good publication (at least neuroscience nowadays) these numbers are incredibly low. Unless there is private money, top end research will be difficult to sustain from NIH funding only.
In the end we should not use additional proxies for MERIT. We should strive to improve review so that the most meritorious science gets funded.
Although I have very little to add to the many good comments above, commenting here is more of signing a petition to stop the proposed point system or at least to think through it very carefully prior to arbitrarily assigning points. After seeing this point system, my first thought was to give up on our MPI grant (where my contribution is crucial) and my second thought was to stop working on P01 with three other junior/mid-carrer PIs. This new approach will kill the collaborative research! The log scale in Figures 5 and 6 masks the real correlation between $$$ and productivity. This is not to say that at some point the correlation stops being linear, but 3 average R01s (roughly equal to $600-700K direct costs) cannot be that mark!
Importantly, please provide those graphs for intramural funding! It is absolutely important that we see the intramural data.
As many others have noted, the intentions of “spreading the NIH wealth” are good, but this particular point system will discourage collaborations, multi-PI grants and participation in large projects when the $$$ is not large enough to justify the penalty points. Furthermore, this point system will discourage submitting training grants which offer no salary support for the PI and no support for the lab, but are still penalized with 2 and 1 points, depending on whether they are single PI or multi-PI. In addition, there is a danger that if someone has a large grant or multiple grants expiring in a year, they might end up with gap in their funding, which can be devastating.
I am curious why, instead of the point system, the NIH does not implement another of the recommendations of the panel, which was to set a minimum % effort to those grants that someone is PI (e.g., 15-20%). This can be combined with a reasonable overall cap of 80-85% effort on all grants combined. Such a cap is reasonable, because essentially everyone has additional obligations (e.g., teaching, administration, committees, working on new ideas for future grants, etc) and they need to devote some time on them too. These too combined can have the same effect of limiting the total funds to a single lab without being too restrictive and punishing collaborations.
There are several “artificial” systems that could enhance apparent productivity, and therefore skew every graph presented. This NIH does not exist in a vacuum.
** How does one metric in the money an HHMI investigator gets?
** How does one metric bio-pharmaceutical collaborations, which can bring in millions of dollars, but might be a “fee for service” arrangement?
** Donations and endowments?
** Foundation support?
As to productivity per se that appears to be lacking in the graphs:
** Are papers the only metric to be used?
** What about products licensed?
** Technologies created for use by others?
** Software created?
** Companies started to translate discoveries?
** Graduate students or postdocs who went on to good jobs (whether academics or industry)?
** Patients saved?
Enormous focus has been on scoring people in collaborative grants for interaction. The point system here destroys the incentive. What about admin centers? What about Cores? Are they to be graded equally since Cores are often “fee for service”, but are often required (efficient) for collaborative work on clinical samples.
I am way on the liberal side of the political spectrum, but this proposal is pure communism and flies in the face of everything I was brought up to practice in science. The best science is a competition– not a commune. As others have noted, if one were to grade this proposal– purely on the LACK of scientific soundness– it would get a failing grade. This proposal needs DEEP review before it goes another step.
This is one of the worst proposals I’ve seen in a while. There is no “average” investigator. We were not printed from a machine. Whatever happened to the core of Darwin’s Theory that drive all our work? Survival of the fittest.
Agree fully. Hope your comments and all the others are taken seriously and do not vanish one day. These comments should preclude any move to implement this poorly analyzed and deeply flawed proposal. NIH purportedly strives to cure disease through the best science possible as defined by pier review and not a socially motivated artificial adjustment. The bang for the buck will only go down in so many ways. A decade latter the damage will be realized but with the best and brightest pushed out of academia etc. Good luck!!
While the desire to provide support to young scientists and spread the NIH ‘wealth’ around is laudable, this proposed policy will have a significant negative impact on many established laboratories throughout the country, especially those with translational research. I wish to reiterate and extend the multiple issues raised above regarding the strong disincentive for collaborative science that this policy would raise.
As a translational researcher, every grant I have is collaborative. If this policy goes into effect why would anyone wish to collaborate with me? My research would not be possible without these collaborations. I certainly would not want to ‘waste’ my funding points being a co-investigator on someone else’s grant where I may receive only a small budget at the expense of having one less R01 equivalent.
This policy could also have the effect of limiting innovation and information dissemination. If a lab is capped, and makes a novel discovery that could lead to new funding opportunities, what incentive would they have to reveal this new information until such time that they could apply for new funding themselves? As it stands now, new findings permit new areas and funding opportunities to open immediately- but this policy would effectively prevent that. Take emerging infectious disease vaccine development (i.e. Zika, Ebola, etc) funding for example: Would we want a system where perhaps the very best researchers in these areas cannot apply for funding because they are capped for the next several years? And if exceptions to the rule would have to be granted under these circumstances, how would those exceptions be parceled out? Would they be given to the best labs, only allowing them to circumvent the rules in place for everyone else?
Some possible different modifications of the policy:
1. Limit the cap to apply only to single PI unsolicited applications. Grants funded under RFAs and RFPs should not be part of the cap, as these are NIH directives. Otherwise RFAs and RFPs will likely see a dramatic decrease in applications from the successfully funded/most established pool of investigators.
2. The scoring system could be entirely recalibrated to incentivize collaborative research.
3. To encourage established investigators to support young scientists, collaborative grants including NIH defined young/new investigators and established investigators could not count towards the established investigator’s cap (or both investigator’s caps). (could place an upper limit on this so it is not abused)
4. As stated by others, participation in center or training grants should not count towards caps if they do not include research budget for PI.
5. Not introduce any caps; instead give NIH more research dollars (or increase the pay line) to set up better programs specifically for supporting only young scientists or less established investigators.
A lot of the problems with the proposed point system have already been discussed above. One more for the list is counting an R35 outstanding investigator award like one R01, when it is the equivalent of about 3 R01s.
The notion of redistributing resources using this index metric may actually result in less funding for junior investigators. Study sections and program officers are often outspoken about the idea that young investigators once they get their first grant have to “prove themselves”. This metric system will institutionalize this approach leaving young investigators stuck in the 7 or below index regardless of their productivity while more senior will automatically go and stay between the 14 to 21 index range. The concept of junior/young investigator keeps getting pushed forward and now includes forty and fifty-year-old people so unless you are full professor or endowed chair you are considered junior and with a lot prove. For the system to truly work or at least be neutral to young investigators it has to include a categorical threshold. By that I mean that points could be counted but could not be used by study sections or councils to influence funding unless they go above 21.
The above comments cover many of my concerns, which, to use study section parlance, greatly diminish my enthusiasm for this proposal. I will echo that assigning points to T32 PIs simply defies logic. As one myself, I can say this is a time-consuming labor of love and a pure service to the education mission of the university and the NIH. A point penalty would drive many even further away from taking on such a commitment. I agree with some proposals above that T32 PIs might get a -2 point bonus for their service. Also, metrics based on literature citation counting raise the hair on my back of my neck. These have been proven to be flawed proxy’s of impact, perverse incentive drivers, and prone to unintended (yet often predictable) consequences. And the data given in this post don’t seem to make the case for a 3 R01 cap in any event. Conclusion: scrap this, please, and start over with peer review scrubbing. PS: I echo the concerns about collaborative multi-PI program disincentives.
One more thought: with age, investigators may change their publication behaviors, as there is less pressure to publish a target number of papers per unit time, and more pressure to make an impact/leave a legacy, etc. Might be interesting to look for signals of such behavior changes in the data, and any new policy certainly shouldn’t apply a penalty to such shifts. The above comments drawing attention to the hit translational science might take under this proposed policy are worrisome in this regard.
I echo many of the concerns above, and hope that this policy is scrapped.
My biggest concerns:
It appears that this policy seeks to actively discourage collaboration. If 2 or 3 investigators share a R01, that R01 is suddenly worth 12 or even 18 points collectively, with each investigator collecting 6 points each. This makes no sense, give the typical resource distribution. This will have an immediate effect of limiting MPI applications. I guess those of us who already have such grants are in trouble.
Even if the policy were to go into place, the points should be better aligned with resources (read money). 5 points seems too much for a R21 given the limited time and scope relative to a R01 at 7 points. This will also immediately discourage smaller R01s (as why would you take a 7 point hit for a modular R01).
Particularly with R21s and R03s, which are time-limited, this will make researchers vulnerable to gaps between funding, since they ‘use up’ a significant amount of points but end quickly, making it harder to sequence grant submissions to maintain that optimal 21 all the time.
I fear this policy will adversely affect physician scientists the most–an already endangered group. Physician scientists are more likely to be in entirely soft money positions where they have to cover a significantly greater percentage of their salary on grants than their colleagues in basic science departments.
I agree with all the concerns raised here, but I am also VERY curious to “get under the hood” of the points system in Table 1.The team developing this index should provide and be prepared to defend the rationale behind assigning 6 points per PI for multi-PI grants. As others have noted, that will have a chilling effect on collaborations. Assigning any points at all for T32s and R25s is a terrible idea. I gather that the points were partly developed with the idea of how much time a PI supposedly spends, but for training and educational grants, that doesn’t match reality. It certainly shouldn’t be a consideration when deciding whether or not to fund that PI’s next *research* grant and will make it so much harder to recruit faculty to lead those efforts! I also agree that the total dollars per PI or per project and actual % effort on the grants belong in the metrics. Spreading the wealth should be part of the funding decision so we have a broad base of research activity, but this proposed points system needs extensive revision. (If limiting PIs to $1M isn’t working –
which seemed more fair – then why is that the case?)
Training and education grants should not be part of this scheme, since they can only be led by more senior people, and have very little support for the PD or administrative infrastructure. I agree that these should trigger bonus points, if the idea is to give junior folks a leg up.
This is very important work. I sincerely appreciate the thorough and thoughtful discussion of the data. While I can see the point of the comments above concerning use of log scale on the Y-axis of some figures, the larger point holds: above an RCI of 21, productivity sags. This is logical, as managing such a large group could easily come with diminishing returns.
I would also like to support the idea of having very low RCI scores assigned to training grants and core support grants. These are critical tools for supporting research but offer little benefit to the PI.
Please do not penalize PIs who have taken on the added responsibility of overseeing a T32 training grant for their institution. Because of the way the point system is structured, just those 2 points will end up reducing their own grant support by one full R01 in many cases. This is a great way to de-incentivize investment in training future generations of scientists.
I also echo the criticisms raised above about the point values for R21s and multi-PI grants. Again, this is a great way to de-incentivize collaboration.
Ultimately, I would argue that this point system is drastically oversimplified and fails to consider the numerous variables that impact how much effort actually goes into a given project. Clearly the activity code alone is insufficient. The approach presented is inherently flawed and should be reconsidered from the ground up.
The point system seems to have a number of flaws as many others have elegantly pointed out. If the goal is to spread the money out among more researchers, the capping of number of R01s one can have, capping of % effort, capping of R01 grant amounts may be a more equitable way to accomplish this goal.
One concern that I have with this point system is that it assumes that every R01 is equal. In reality, the direct costs on an R01 can vary between $170K and $500K per year. Further, Multi-PI R01s have become increasingly common, scenarios that often leave each PI with anywhere from $50k to $150K.
With that in mind, wouldn’t it make more sense to focus on the resources available to the PI? If being a PI on an R01 is always worth 7 points, a person could reach 21 points with relatively limited resources. Further, substantial resources would be available to labs able to write large non-modular R01s.
I completely agree.
In fact I was preparing to submit a joint RO1 for next week, but today I had to cancel last second upon reading this note. If this goes through it would make it impossible for me to renew my own RO1 and I could not risk that.
If the NIH wants to spread out the funding, then please do not use an unreliable proxy for the dollar amount. A single RO1 is 7 points, and sharing three RO1s in three ways — greatly improving collaborations while receiving the same dollar amount — is 18 points. Ridiculous.
Either make it about the actual dollars or lower the points for shared grants.
It seems that the NIH is determined to implement this very flawed system since Dr. Collins announced the start of this program in his testimony to Congress this week. Hopefully he will heed the extensive feedback from the scientific community pointing out that the proposed scoring system needs to be revamped to prevent it from acting as a severe disincentive to altruistic and collaborative activities. These are legitimate concerns and not simply the rich seeking to protect their prerogatives, as some advocates of this proposal have disparagingly declared.
According to Dr. Collins’ testimony the motivation for this radical change grant funding, with it’s implicit distrust of the current peer review mechanisms, is a desire to help new investigators. Let’s take him at his word. As a Department Chair, I have a witnessed first hand how destructive the current system has been for Junior Faculty over the last 15 years. But sadly, in my opinion, simply channeling a few percent of the resources from the R01 pool back into the black hole of the general competition, at the expense of the most successful scientists in the country, will do nothing to substantially help Junior Faculty develop or help to advance the best science, which requires variable levels of resources.
Here’s what the NIH could do if they are serious about fostering a new generation of world-class investigators: Create a structured program to help build the careers of the most promising early stage investigators. I would recommend that the NIH initiate a starter grant mechanism, which is separately reviewed and properly resourced. This could be, for example, a 3 year grant funded on the R01 scale. The starter grants could have a mentored element built in and there should be an expectation of matching funds from start up packages, so the Universities have some skin in the game. These types of programs have been tried in the past and have deemed to be failures because the conversion rates to R01s have been poor. However, the earlier programs were inadequately resourced, lacked a mentoring component, and most importantly, lacked a structured second phase. I therefore recommend that the initial 3 year phase be followed up by a second phase which results in a regular 5 year R01-sized grant. Once again, these grants should be reviewed separately from the total R01 pool. The standards for the second phase could be very rigorous, since the idea behind the program is to foster excellence, not to provide sinecures, but the main criteria should be career progression and innovation rather the minutiae of the research proposals. Perhaps there will be a limited success rate at this stage. We live in a meritocracy, and not everyone will become a leading scientist. At some time during this second phase the participants should be encouraged to apply for a second R01, since this is where the biggest increase in productivity is achieved. These grants should be considered and scored in the regular study sections but given a suitable priority advantage to ensure that a reasonable fraction of them get funded. After that, everyone would be on their own and in the open competition. There is an implied 10 to 15 year commitment inherent in this scheme, but that is realistically what it takes to breed mature scientists.
Personally, I would be happy to pay my tithe if I knew it would support a program of this type. However, to disrupt the best laboratories in the country for the sake of throwing a very limited amount of money into the bottomless pit of the open R01 competition seems to me to be absurd and counterproductive. Worst of all, it squanders an opportunity to protect our nation’s most precious resource, which the next generation of scientists.
The point allocation proposed for Multi-PI and multi-component grants strongly disincentivizes team science. Grant-funded projects which bring together senior scientists, technical experts, and/or clinicians from different fields lead to multidisciplinary approaches with several individuals with different expertise working together in complex projects. These types of approaches are critical to making progress on difficult problems and should be encouraged, not discouraged, by NIH policy. The resources available to a multi-PI are quite limited and this scoring would unfairly penalize scientists who are working collaboratively. One alternative would be to divide the points value by the number of PIs (and possibly add 1 point, i.e. (points/n)+1.
I applaud the idea of limiting grant funds to individual investigators as a way of “spreading the wealth” to numerous investigators and better engaging our younger scientists in NIH funding. However, the point system as devised is severely flawed. I agree with the previous respondent that the point allocation disincentivizes team science at a time when the need for multi-PI teams of science is at its greatest. The best science brings together disparate ideas to generate novel lines of inquiry and multiple approaches to attack them – this is best done through multi-PI and multi-component grants. By giving nearly equal weight to a co-PI of a multi-PI grant as to a single PI, however, you would be essentially double-charging and penalizing collaboration. I have heard the notion justified on the thought that most multi-PI grants have double the budget of single PI grants, but I contest this notion. For example, most of my funding is from mutli-PI grants, and nearly all of those grants are at or near modular budget level; from one on which I am a co-PI, I bring in barely over $50,000 in annual direct costs for my own group. Thus, although my current point value would exceed the maximum allowable, my total lab budget is well below that of a PI with three modular grants. I do not think that I am unusual in this respect, and of many multi-PI grants that I have reviewed at study section, few – if any – would support any single PI with as much funding as a modular grant for a solo PI proposal.
A point system should be tied to the actual direct costs that an investigator receives rather than to an arbitrary number of grants. After all, the NIH budget is dictated by dollars, not by the number of grants given, and we pay our bills with dollars and not grant vouchers. I think that PIs can largely be trusted to be honest about their “take” from multi-PI grants to allow for a fair and equitable distribution of NIH funding.
I want to echo the concerns about collaborative proposals; this proposal as written would provide a strong disincentive to collaborate.
That said, I have sympathy for the desire to make the system somewhat more egalitarian. An alternative approach would be to have a total number of points per grant and then distribute those among the PIs/Co PIs based on relative levels of support / effort (or perhaps by allowing them to allocate the points as they saw fit). There might need to be additional digital documentation so that it was easy to look up an investigator’s point commitments, but the result would strongly incentivise collaboration, and would maintain the general sense that an R01 is to support a particular amount of science, regardless of how many investigators are involved.
It seems that the scale generated and the the discussion provided in the blog focus on the number of RO1 grants an investigator holds. However, I wonder if the data regarding the fall off in productivity when moving to 3 RO1 from 2 RO1 are applicable to investigators with a high GSI who have a more diverse portfolio of NIH support? In other words, is it possible you are applying your process too generally?
The entire premise for the GSI limit proposal is ironically based on a misinterpretation of the data presented on the relative citations versus points graph. The y axis is a log10 scale and while the x axis is not linear, it is not nearly as compressed as a log10 scale. The “straight line” drawn to represent linear productivity is actually an exponential increase. If the graph were drawn in a more easily interpretable linear scale – it is easily seen that PIs with multiple grant are actually much more productive than those with one RO1.
This serious mistake undermines the entire basis for the NIH GSI limit. The proposal point cap has serious flaws that will cause major damage and disruption to the leadership enjoyed by the United States in biomedical science – and this will ultimately cost lives both in the US and world-wide.
The current system is based on a meritocracy, as science should be. Let the best science surface. It is also democratic –based on evaluation by our peers. To cap the best ideas and science is un-American and make no more sense towards achieving any scientific goals than removing a star athlete for the line-up once he/she scores a certain number of points.
There are a number of major problems in the proposed point system that will be highly detrimental to training, collaboration, and innovation – the cornerstone of scientific endeavor:
1) Charging points for a T32 will make many reluctant to sponsor such a grant. This will choke the training of new scientists.
2) Charging more points for being overall PI of a PO1 than an RO1, will kill the PO1 mechanism. The overall PI really gets no more for his/her efforts than for an RO1(which can be have non-modular budgets) – and clearly no more than individual project leaders. The PO1 mechanism is a way that many of us who run smaller labs (under the 3RO1 limit) to collaborate with bigger labs and DUE TO SYNERGISTIC INTERACTIONS, accomplish more than individual RO1s. This collaborative and synergistic mechanism will be penalized and will falter under the proposed point system.
3) Charging co-PI’s (on multi-PI grants) points that are not commensurate with the amount of support obtained, will limit co-PI grants – another mechanism by which labs collaborate (and large well-funded labs and spread their talent towards joint efforts – to the benefit of all involved.
4) Large well-funded labs are not only more productive (see above) but are more innovative – indeed they produce more high profile manuscripts and “big science” approaches that small labs cannot. There is an “economy of scales” that allows larger labs to do more with the money than a single RO10fiunded grant. Importantly, large labs perform other critically important services to the community. First, they collaborate with smaller labs – spreading their expertise and innovative approaches. Second, they teach a large number of post-docs in cutting edge science – the next generation. Shifting more of these responsibilities to researchers who are less successful (less scientifically competitive proposals) – is inherently pushing science and training towards the mean as opposed to pushing the exceptional.
5) As scientists, we get funding for only one grant on a given topic. This encourages us, as we develop our careers, to keep our eyes open for new ideas. In turn, this promotes movement into new areas and development of new paradigms. Current funding encourages exploration outside of the initial areas we are funded in. But if working in such a new area means giving up funding in an area where we are most comfortable, we will be reticent. This will occur even for PIs who are carrying two RO1s and T32, or a RO1 and a PO1. They simply will not follow scientifically interesting and potentially important leads because they cannot get funding for it. Most of what my lab is funded for now is based on findings that I followed up on – and some was performed when the new work would have put me over the point-cap (due to a PO1 or T32). The new system will be scientifically stifling. New leads will be missed and new discoveries lost – to the detriment of disease-oriented science.
6) The point system will not benefit new investigators or those who cannot get their first RO1. It will simply remove funding from the most highly funded labs those who are most successful and allow those in next tier of scientific success (e.g. those with 2 RO1s) to obtain a third.
7) The most competitive big science labs will carry less RO1s – but will justify bigger budgets, limiting the amount of funding to other labs.
In summary, the entire idea for this radical change to funding US scientific endeavor is built on a faulty premise resulting from a poorly drawn graph. It should be withdrawn. The scientific community should be engaged to develop a system that promotes investigator-initiated research and does not punish the most successful scientists, inhibit training, and stifle innovation.
The overall rationale behind the NIH Grant Support Index proposal is something I agree with, as an early-career scientist. This will open positions for new independent investigators, and allow small labs to expand, ultimately resulting in an increased diversity of ideas and science funded by the NIH.
However, I would like to point out at least 3 items that should be refined before the policy is enacted.
First, on the topic of training grants and fellowships: there should be no points assessed to mentors on these grants (or even negative points!). This will cause PIs to discourage their students and postdocs from applying to F series grants, as they carry no research support money. Further, considering the fixed (and anemic) indirects of the F series, they will be discouraged at an institutional level–why take an indirect shortfall while increasing your GSI number?
Second, on the topic of multiple PI penalties. The NIH is stronger through collaboration, and multiple PI grants. PIs should not be “punished” for collaborating. It seems the most balanced approach is to scale the points assigned to multiple PIs by the percentage of funds in the budget (and perhaps subtract one from that number-to encourage collaboration!).
Finally, a serious shortcoming of the GSI as proposed is potentially crippling our response to health crises or emerging diseases. For a specific example, the incredible development of multiple successful vaccines for Zika virus by the laboratory of Dan Barouch would not have been possible if the GSI had been in place (he confirmed this to me in conversation). However, the considerable resources and infrastructure he had in place as a leader in HIV research were quickly repurposed to address a new health crisis. I would recommend that the GSI be modified to allow specific “crisis response” RFAs, specified by the NIH, to be assessed zero points. This would allow for the nimble reaction to emerging crises.