10 Comments
In March 2017, we wrote about federal funders’ policies on interim research products, including preprints. We encouraged applicants and awardees include citations to preprints in their grant applications and progress reports. Some of your feedback pointed to the potential impact of this new policy on the peer review process.
Some issues will take a while to explore as preprints become more prevalent. But some we can dig into immediately. For example, how do references cited in an application impact review? To start to address this question, we considered another one as well: do peer reviewers look at references – either those cited by applicants or others – while evaluating an application? We had heard anecdotes, ranging from “Yes, I always do,” to “No, I don’t need to,’ but we didn’t have data one way or the other. And if reviewers do check references, how does it impact their understanding and scoring of an application?
So, together with colleagues from the NIH Center for Scientific Review (CSR), we reached out to 1,000 randomly selected CSR reviewers who handled applications for the January 1, 2018 Council Round. There were an equal number of chartered (i.e. permanent) and temporary reviewers solicited to participate (n=500 each) over a three week period from November 16 to December 8, 2017.
Our survey focused on the last grant where they served as primary reviewer. Specifically, we asked if they looked up any references that were either included in the application (i.e. internal references), and if they also looked up any that were not included in the application (i.e. external references). Depending on their answers to each of these questions, we also proceeded to ask certain respondents follow-up questions to better understand their initial feedback. We felt it would be interesting to know, for example, how reading the paper or abstract impacted their understanding of the application and their score.
We received 615 responses (62% of total), including 306 chartered members and 309 temporary members. Figure 1 shows the responses related to if they looked up references, either internal or external to the application. Most reviewers answered yes – particularly for internal references.
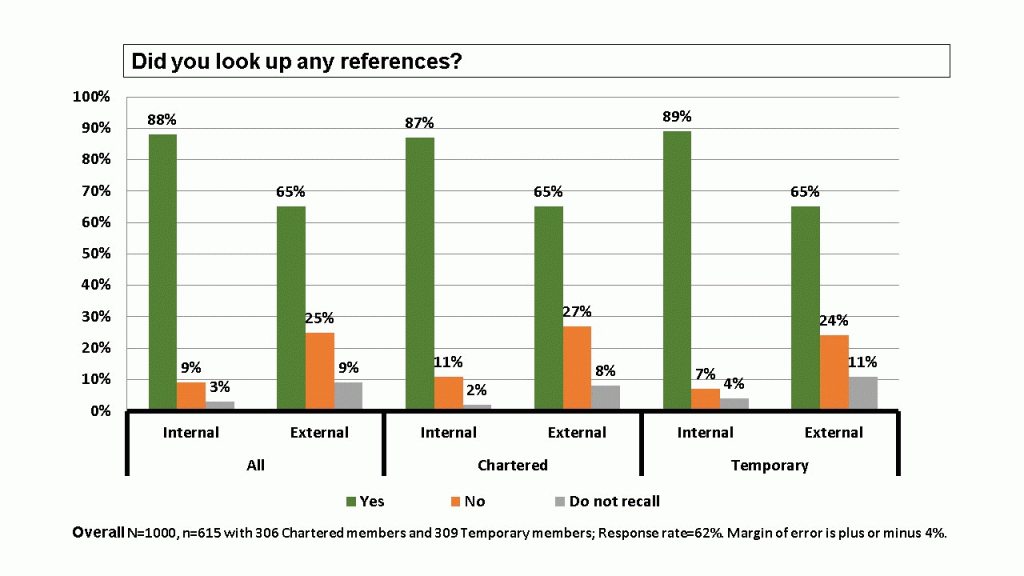
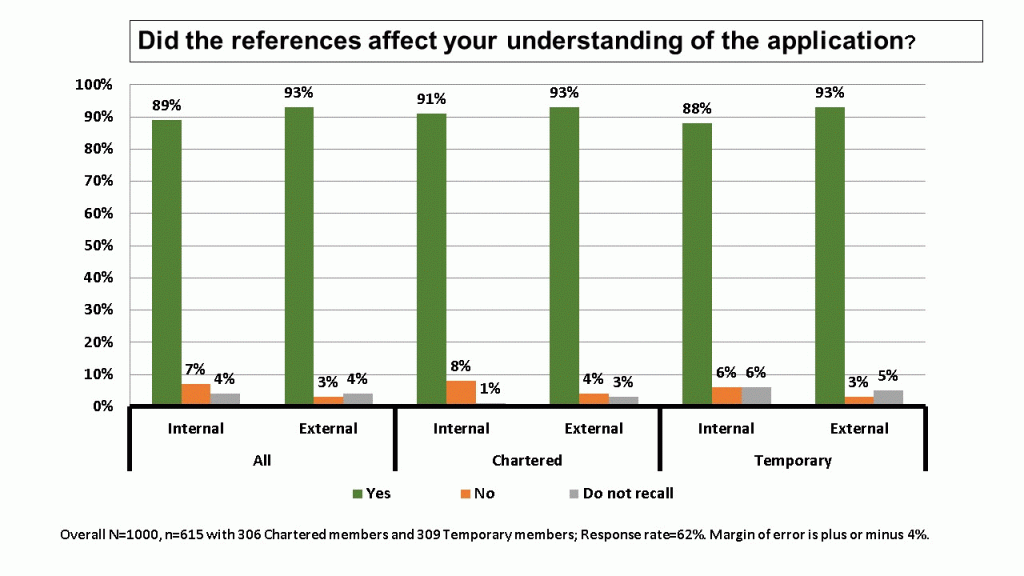
Figure 2 goes a bit deeper – as a secondary question, we asked whether the references affected reviewers’ understanding of the applications. The clear majority said yes. Figure 4, shows that most reviewers (~85%) found the references improved their understanding.
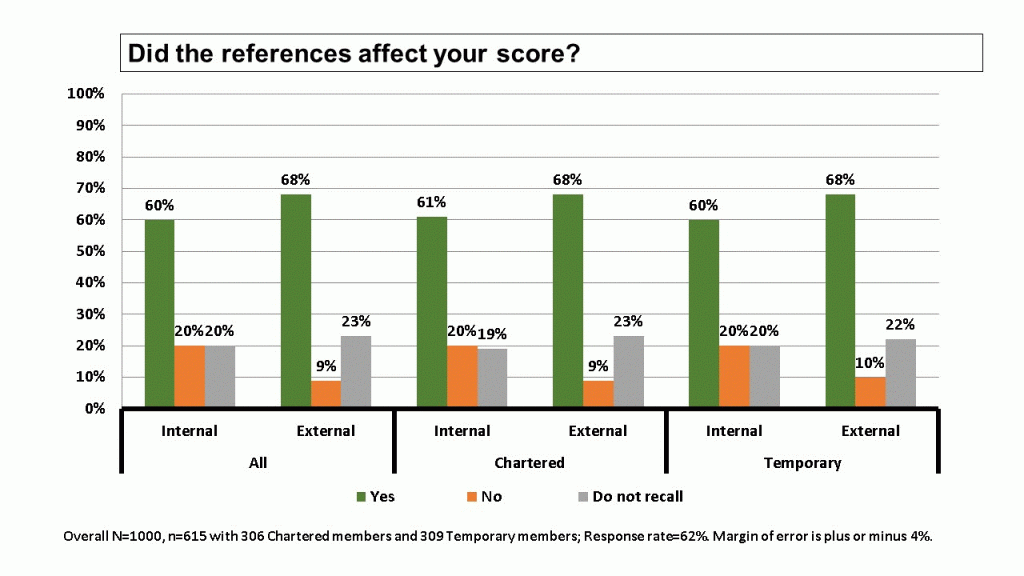
Next, we learned that of those reviewers that checked references, about 2/3 reported that the references affected their scoring for the application (Figure 3). References reviewers found on their own (external references) seemed slightly more influential. Figure 4 shows references could impact the score in either direction. References cited in the application were slightly more likely to improve scores than worsen them, and external references were slightly more likely to make scores worse than improve them.
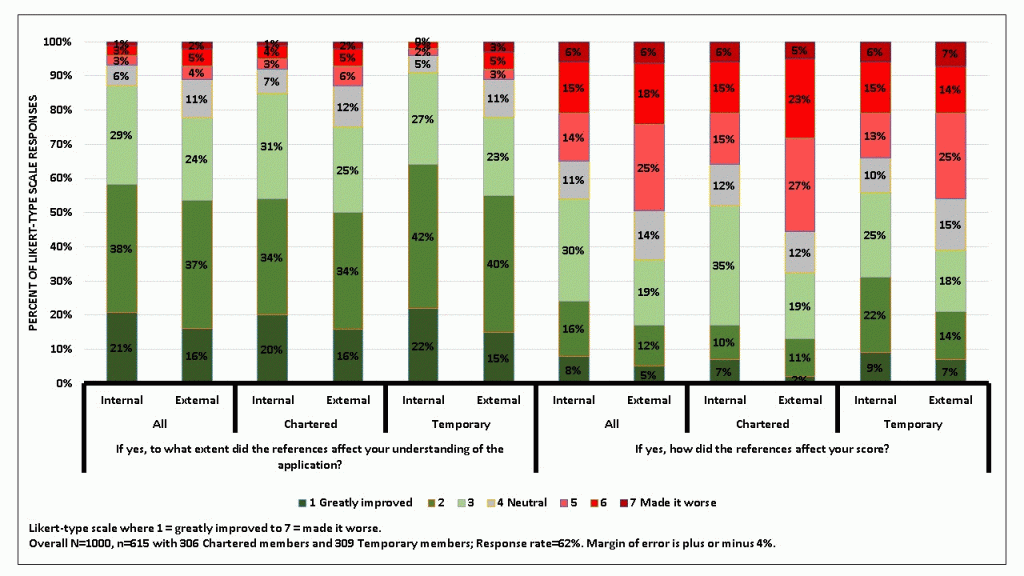
Nearly half of the respondents even provided additional comments for us to consider. Here is a sampling of their thoughts:
- “References are of immense value.”
- “I look up references to judge the quality of the [principal investigator’s] work in relation to the rest of the field, to learn about the field in general, and to delve into specific questions that might be key to evaluation of the application. This could result in changes to the score in either direction.”
- “References are useful and sometimes critical.”
This experience was very enlightening. We were pleased to learn that most reviewers do look up references as part of their work in the peer review process, but preprints, at least for now, are too rarely cited in applications to have a clear impact. Further, both chartered and temporary reviewers shared similar perspectives on looking up references, which they noted often affects their understanding of the applications and resulting scores. Finally, they indicated that references internal to applications often lead to reviewers’ improving their scores. We may need to revisit this survey as preprints and other interim products become more common.
Overall, this survey demonstrates, yet again, the time and care NIH reviewers spend on applications. They work hard for all of us- NIH, applicants and the American public, and I am personally grateful to all of them.
I would like to acknowledge Neil Thakur with the NIH Office of extramural research as well as Mary Ann Guadagno, Leo Wu, Huong Tran, Cheng Zhang, Lin Yang, Chuck Dumais, and Richard Nakamura with the NIH Center for Scientific Review for their work on this project.



As a chartered member of a standing study section and frequent ad hoc reviewer for SEPs, I view both internal and external references as critical in determining the novelty, impact and appropriateness of approaches for a given application. For certain application, I probably spent nearly equal amount time in reviewing both the proposal itself and the relevant literature so that I can fairly and objectively review the application.
Where CSR and NIH can help us reduce the burden is in the biosketch section to list: 1) most relevant publications by the applicant to assess the contribution as well as scientific basis of the application; 2) selected most recent publications (3-5 pubs in 3 years for example) to assess the recent productivity as well as trajectory of an applicant. With the current format, in the contribution to science section, it is hard if not possible sometime to find these information. One could spend substantial amount of time digging through PubMed for these important references to informatively review the relevant sections of a given proposal.
I have also served on many study sections and agree completely with your suggestions but I would take modify it so that the 3-5 publications would be the most relevant to the project rather than being restricted to the most recent. Also, it would be a huge to go back to old systems of included the applicants’ most relevant publications in the proposal. It should be very easy to allow pdfs of the publications to be included in the application vs doing it w/ paper copies as was done in the old days.
Please provide clarity on how use of external references is appropriate. If reviewers are required to review an application based on what is in the application, how can references that are not cited be considered as legitimately informative?
Looking up the references their credibility is as important as application itself. A lot of times the references in the application and in the bio-sketch can be deciding factors in scoring the application.
A related question would be whether the weight of references are reflected in the summary statement – i.e. do reviewers routinely report where a deficiency of references or perceived conflict (or agreement) with cited papers was important to their appraisal of the proposal. That would be considerably more helpful to submitting scientists…
An important aspect of the use of references in grant applications that I did not see mentioned in the article or comments is the potential to use cited references from the applicant to get around page limitations. I believe it is simply not fair for an applicant to omit key data in an application by citing a recent publication and sending reviewers to that published work for details. On the other hand, when I feel uncertain about key aspects of a field, method, or other aspects of a proposal of course I go off and research it, including using cited references. I think this is an important distinction that reviewers should keep in mind.
While I do not doubt NIH reviewers take time to review internal and external references, I wonder if this is an indication of conducting and receiving a quality review.
The numerous summary statements myself and my colleagues have received over the past many years that include misspelled words, poorly structured sentences, and/or a complete lack of clarity or detail of the weaknesses identified, are among the many indications of the limited attention/time spent on conducting a thorough (and quality) review. Over the years I have also interacted with a number of reviewers who are completing their reviews the day they are due. Also, I have served on many study sections where, at the opening of the read phase, numerous reviewers have yet to submit their reviews. I believe indicators, such as these, could be used to more effectively determine the quality of a review and to better understand how much time is committed by reviewers when conducting a review.
I also have reviewed NIH and applications from several other agencies including foreign Government applications.
1. The time a reviewer spends on a review has no bearing on the quality of the review. If I am extremely familiar with a topic and literature, I spend as little time as possible on that application as opposed to the time I spend on a less familiar topic.
2. Typos, spelling and grammar of reviews should not be a factor in deciding whether a reviewer was good or bad. Nowadays, it is common to see quite a few reviewers for whom English was a second language. Are they bad scientists? Are we to conclude that a reviewer spent very little time on an application, because of bad grammar and typos?
3. On the same basis, unless incomprehensible, is an application written with typos reflect the quality of science?
The precision that many reviewers use researching references is rewarding, but the high noise level in the funding process (where you need to reject about 90% of your applications), suggests that precision in a review may not be the same as accuracy.
About 40 million applications are rejected each year by NIH and if you figure the time expended by those applicants and a mean rate of pay, the rejected applications cost taxpayers nearly $2 billion/year and that should be part of NIH expenses for running the system.
Sorry, but too many reviewers, like restaurants and airlines, tell lies to defend their pride and position on a panel. We can tell that our publications are seldom read, and our applications are seldom read with care and unbiased openness to innovative ideas. We thank the CSR for taking on a very difficult job to recruit willing reviewers with appropriate background. Smaller panels with truly dedicated reviewers in the face-to-face setting would improve the overall result quality.